循证·解读,赋能问题化学习数活动
——以大班数活动《老狼老狼几点了》为例
上海市宝山区密山幼儿园 徐莉 李文勤
“学起于思,思源于疑”,问题化学习的课堂总是给孩子们带来无限可能。以大班数活动《老狼老狼几点了》为例,通过前后两次集体教学活动后相关课堂数据的比较分析与调整,可以发现课堂循证将科学有效的信息用到实际教育教学课堂中,助力问题化学习活动质量,赋能幼儿学习的潜能。
大班数活动《老狼老狼几点了》的活动目标是:
1.通过解决游戏中出现的问题,巩固幼儿单双数的经验。
2.理解游戏的玩法和规则,体验合作游戏带来的快乐。

在这个环节中,教师和孩子们讨论并引出今天活动的主题。通过出示羊和狼的头像以及塑料圈等游戏材料,与幼儿共同谈论,明确游戏名称和游戏规则。教师采取了以下的方式:
做法1:
(教师)猜猜今天我们要玩什么游戏?
(幼儿)
1.喜洋洋的游戏。
2.掷色子的游戏。
3.关于数字的游戏。
(教师)今天我们要玩老狼老狼几点了的游戏,谁还记得怎么玩?
(幼儿)
1.羊在天黑的时候要躲进房子里。
2.我们要念儿歌问老狼几点了,听到天黑了小羊要逃。
3.小羊是要逃进这个圈里吗?
效果:在这个环节中,教师设计的两个问题是比较开放的,孩子们也猜到了今天可能会玩与羊、数字有关的游戏,但是激发孩子提问的引导还不够,所以整个环节中只有一名幼儿有问题“小羊是要逃进这个圈里吗?”。游戏玩法与规则以教师交代为主。

在这个环节中通过掷色子,决定每一轮游戏中小羊的数量,幼儿根据羊圈中小羊的数量,并运用已有的数经验,判断本局胜负并用点卡符号进行记录。师生共游戏了五次,分别是:4、8、10、7、6(小羊赢4次、狼赢1次)。以下是教师的关键引导与活动效果。
做法2:
(教师)圆圈中有两个点代表什么意思?
(幼儿)
1.圆圈代表呼啦圈(羊圈)
2.圈里面的点子代表小羊的数量。
第二轮:8只小羊来游戏
(教师)这次是谁赢?为什么是小赢了?
(幼儿)
1.因为两边数量都是4,所以小羊赢了。
2.我希望老狼能赢一局。
3.老狼不会赢的吧?
第四轮:7只小羊来游戏
(教师)色子投到7,你们觉得是谁会赢?
(幼儿)
1.我觉得老狼赢,因为4加3等于7。
2.这是7最中间的分法了,所以两个羊圈是不相等的。
效果:在这个环节中,教师提出了是何与为何的问题,抓住了学习的核心,能够验证不同数量小羊的输赢结果,并以图示记录,找到了小羊和老狼胜利的原因。尽管目标达成,但是孩子自主提出问题依旧鲜见,学习过程始终还是教师主控。

第三环节主要让幼儿通过观察前几轮的比赛结果,提出自己的疑问,在解决问题的过程中发现小羊的数量(双和单)与输赢结果之间的关系。
做法3:
(教师)小朋友,看看这样的游戏结果,你们有什么问题要问吗?
(幼儿)
1.为什么每一次玩好羊圈里的数量是不同的?
2.为什么狼的数量要和小羊的数量分开放?
(教师)为什么7不能让小羊胜?
(幼儿)
1.因为7是单数。
2.小羊获胜的数字都是双数。
效果:这个环节中通过让幼儿观察输赢比赛的结果,发现活动输赢的规律,但是从2名幼儿提问的内容中可以发现,幼儿提出的问题和课前预设的核心问题“理解、区分单数和双数的经验”还是有一定距离的。
以上是活动的三个主要环节,通过导入课堂循证平台,得到以下课堂数据:
从图中我们看到了活动中高频词在剔除“小羊”、“狼”、“游戏”这三个游戏术语后,我们发现高频词“双数”、“单数”分别出现了14次和11次。
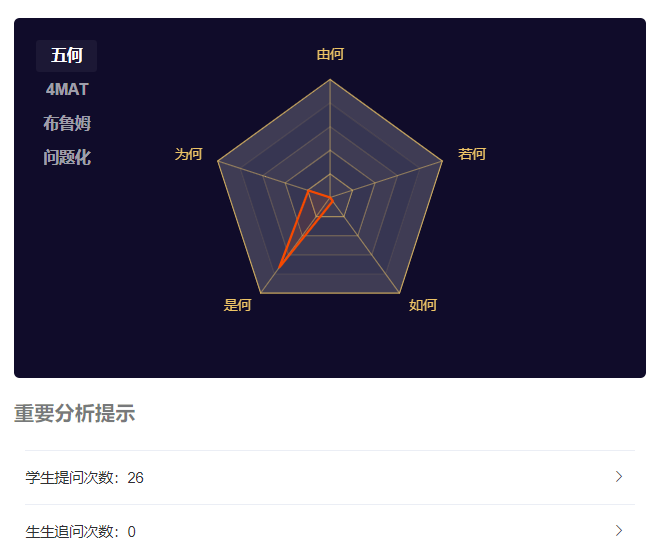
从图中我们发现本次活动幼儿的提问次数为26次,提问的方式相对集中在“为何”“是何”的问题,且许多问题游离在目标之外。
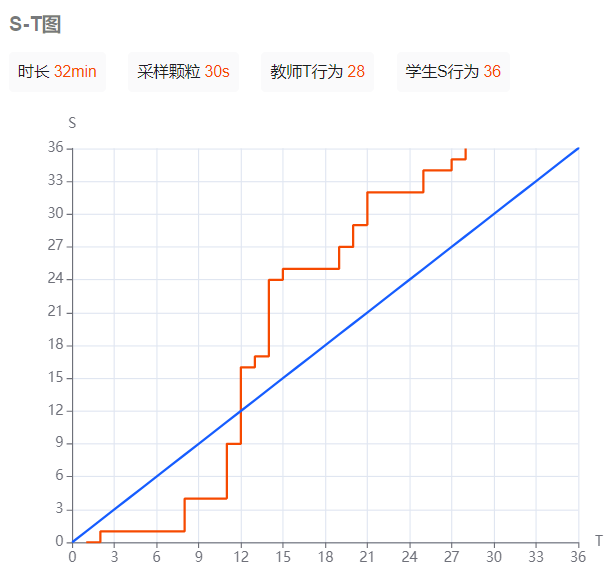
1)S-T图
从s-t图表中,我们发现师幼互动中教师行为:28次,学生行为:36次。在活动的第一环节阶段,红色的曲线在蓝色直线的下方,表示教师更占主导地位。
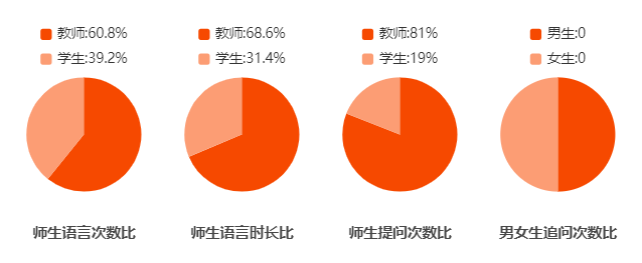
2)师生语言分布图
从下图中反映出教师语言时长占:68.6%,学生:31.4%,师生提问次数比:教师占:81%,学生占:19%,学生提问不够活跃。
从第一次试教的循证数据中,我们发现教师在活动中的语言时长、提问次数远远高于幼儿,说明幼儿主动学习还不够,特别是:
1.教师的开放式提问,为什么没有激发幼儿提出高质量的核心问题?
2.在观察了游戏记录后,幼儿为什么找不出关键问题?
基于第一次试教后的分析与反思,我们对环节进行了优化,接下来我们进行了第二次试教。
第二次试教
在第二次试教中,对教学设计主要做了以下两个调整:

在第一环节中,我们采取了让幼儿关注材料+开放式提问的方法,激发幼儿提出更多有效的问题。
做法1
(教师):今天我们要来玩一个游戏,看看今天老师带来的材料,你们有什么想问的?
(幼儿)
1.为什么有喜洋洋和灰太狼?
2.是不是要丢色子才能玩?
3.为什么地上有两个圈?
4.是不是要有人做羊,有人做狼?
5.两个圈要怎么躲呢?
效果1 :从调整后的环节中我们发现,当关注了材料后,幼儿的提问数量变多了,有5名幼儿提出了问题,并且提问的方式也丰富了,有“为何”的问题、“是何”的问题、更有“如何”的问题,提问的内容变得更聚焦于游戏玩法。

在在游戏的过程中,我们利用游戏材料给幼儿制造思维冲突,产生了意想不到的学习效果。
做法2:教师提供了两个不同的色子分别是单数色子和双数色子,游戏一开始先出示单数的色子让幼儿进行游戏,在反复游戏了三次后,幼儿一次都没赢,激发了幼儿的内心质疑和主动要赢的欲望。
(幼儿):
1.为什么总是老狼赢?
2.老狼真坏啊。
(教师):是呀,为什么总是老狼赢,你们有什么发现吗?
(幼儿):
1.怎么色子都是单数啊?
2.可不可以色出双数呢?
3.2.4.6.8是双数,双数就可以赢了。
(教师):为什么双数就可以赢?
(幼儿):如果色子都是双数,双数可以让两个圈里的羊相等。
效果2:当我们调整了游戏的材料色子以后,故意使用单数色子让幼儿游戏,幼儿在游戏前的想法通常是有赢的机会,但是尝试了多次输的游戏体验。在这样的认知冲突中,疑问随之自然而然的产生了。在调整后,几乎所有的孩子都提出了“为什么老狼总是赢?”的核心问题,并在探究中发现了输赢的规律。
第二次试教后的数据分析
在调整了两个环节的设计后,我们将活动视频导入课堂循证平台,获得以下关键数据:
第二试教中幼儿的提问次数增加到44次,提问的方式除了“为何”“是何”问题,还出现了“为何”的问题——色子怎么都是单数啊?;若何的问题——可不可以色出双数呢?;如何的问题——两个圈要怎么躲呢?
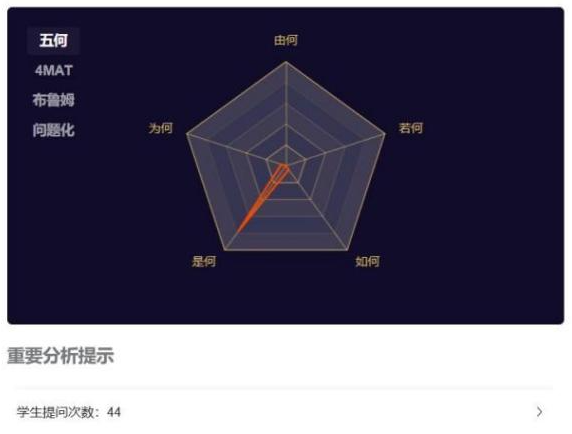
1)S-T图
在S-T图对比中,我们可以看到,第二次的试教中教师行为:27次,学生行为:50次。相比第一次的数据,幼儿的行为有了明显的增加。另外红色的曲线(学生)远远高于蓝色的直线,由此说明活动中幼儿更占主导地位。
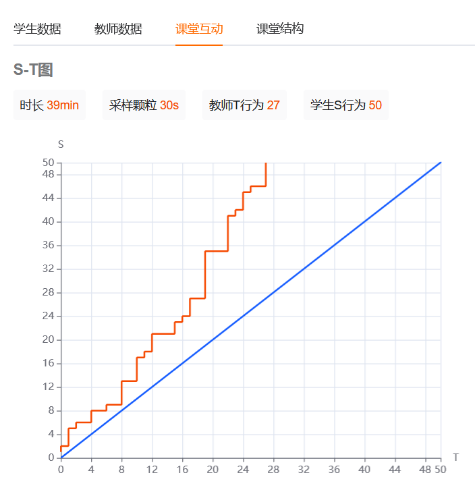
2)师生语言分布图
第二次试教教师语言时长占:64.2%,学生语言占:35.8%。学生提问次数占:21.8%。幼儿的语言时长、学生提问次数在比例上均有所提升。
我们的收获
问题化学习中,问题系统的产生与设计是“以幼儿问题为起点,以学科问题为基础、以教师问题为引导的三位一体”为思考点。因此,我们在活动中要以幼儿为学习主体,设置有效情境,引发幼儿思维发散,并提出问题,聚焦问题,提升幼儿提问能力和提问水平。
皮亚杰认为:认知发展的内在动力是平衡,具有自我调节作用的平衡过程是智力发展的内在动力。当我们给幼儿制造了一定的冲突时,就会打破这样的平衡状态,在幼儿失衡的过程中会激发幼儿的问题,找到解决问题的关键所在,从而达到平衡的状态,这样的一个过程正是幼儿主动建构认知、学习的过程。由此,我们在设计活动时,通过有意识的设置困境、障碍,从而产生冲突、矛盾,激发孩子主动的发现问题、解决问题,让幼儿的学习行为主动发生。
此次,通过联课平台对数活动《老狼老狼几点了》两次试教的数据分析,让我们能及时了解活动现状并进行针对性的调整,从而优化问题化学习的课堂质量。如今,在互联网、大数据与教育深度融合的时代背景下,课堂循证将科学有效的课堂实时数据运用到实际的教育教学工作中,为问题化学习融入幼儿园学习活动,赋予了新的分析视角,让教师能更深入的发现儿童!